CS 184: Computer Graphics and Imaging, Spring 2020

Final Project: Fluid Simulation

Amrah Arif, Nisreen Alqaisi, Shadaj Laddad

Abstract

In this project, we built a particle-based 2D fluid simulation system that runs in real-time in the browser. We used the double-density relaxation algorithm to simulate liquid particle behavior, implemented viscosity for realistic flow, used metaballs to render particles to the screen, and added user interaction support to apply forces to the liquid. We implemented the project with Rust compiled to WebAssembly and OpenGL2, which allowed the simulation to run at 60 frames per second with up to 200 particles.

Technical Approach

Our approach was to break down the physics we wanted to implement to make the liquid act similarly to water into 5 core parts: gravity, particle-to-wall collisions, particle-particle interactions, viscosity, and user forces. In addition, we also used metaballs to render particles to the screen and used advanced web technologies to run the simulation in real-time in the browser.

Gravity and Particle-Wall Collisions

First we added gravity and particle-to-wall collisions. This was just updating the forces, velocity, and positions for every time step using the proper equations for each force. For gravity, this is:

$$F_{gravity} = m_{particle} * -g$$

Once we accumulate the forces acting on each particle, we update the velocity and position using a forward Euler step:

$$v^{(t + 1)} = v^{(t)} + \frac{F}{m_p}\Delta{T}$$ $$p^{(t + 1)} = p^{(t)} + v^{(t + 1)}\Delta{T}$$

to implement wall collisions, we bounced back the particle position to

$$boundary - distance\_surpassing\_boundaries$$

and updated the velocity so that

$$v_{final} = -v_{initial} * fraction$$

where the fraction is added to slow down the particle when colliding (simulating a loss of energy due to the friction).

simulation with particle collisions

Metaball Rendering

When we observe the behavior of liquid in real life, we notice that we can only see individual droplets of water when they are isolated from each other. As soon as these drops of liquid touch each other, they combine to become a larger drop. This is the idea behind why we implemented metaballs. Metaballs are surfaces that are created as individual particles merge together when in close proximity to each other and create a larger contiguous (blobby-looking) object.

The implementation of the metaball algorithm starts off with considering all of the points inside each of the individual particles (represented as circles) on the 2D surface. Instead of treating the particles as independent objects, we consider the contributions of each of the circles towards the final metaball display. For each point on the canvas, we try to see if it lies within a constant threshold distance from the center of any (and often multiple) circles. If it lies within that distance, we consider that to be part of the final metaball surface.

The following equation demonstrates the contributions of the n particles towards the final metaball representation, with the threshold set as 1.

$$\sum_{i = 0}^n \frac{r_i^2}{(x - x_i)^2 + (y - y_i)^2} \geq 1$$ In addition to this core algorithm, we added color by taking a sum of masses of particles weighed by the reciprocal of their distance to the current point and using that sum to linearly interpolate between green (low mass) to blue (large mass).

Particle-Particle Interactions

To implement core fluid dynamics through a particle-based system, we used the double density relaxation algorithm [1, 2, 4]. This calculates forces that act on particles based on neighbors and their proximities to the particle. For each neighboring particle, we calculate its gradient, which is

$$1 - \frac{distance}{radius}$$

where radius is a simulation parameter that sets how close particles must be to interact with each other. Then, we calculate pressure, which is a quadratic function of the gradient, and near pressure, which is a cubic function of the gradient. We then apply a force to the particle equal to a weighted average of the two pressures. A challenging part of implementing this algorithm was tuning all of the parameters to get a good balance between accuracy and stability, since we had relatively high time steps to maintain real-time performance.

simulation with metaballs and the double density relaxation algorithm

Viscosity

Viscosity was then added to simulate the liquid property of resisting flow. We implemented this through a particle-based approximation of the effects of viscosity [1]. First we defined (arbitrarily, until the simulation looked decent) the constants \(\sigma\) and \(\beta\) -- the viscosity’s linear and quadratic dependence on the velocity of the particle. We then updated the velocity of the particle with respect to each of its neighbors within close proximity by subtracting the velocity by an impulse in the following expression

$$I \leftarrow 0.5 * timeStep * (1 - q) * (\sigma * vel_{inward} + \beta * vel_{inward}^2) * v_{p, n}$$

In this expression, \(1 - q\) represents the proximity between two particles which increases viscosity the closer the two particles are to each other.

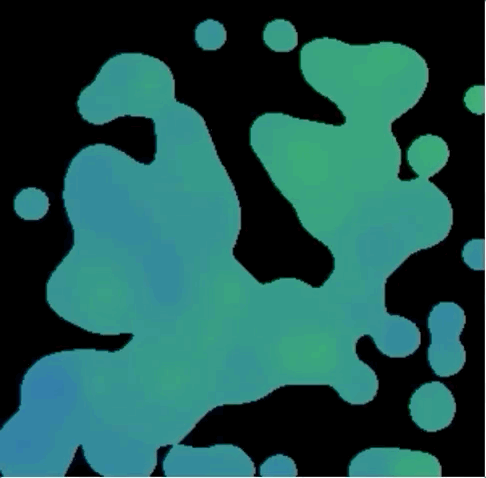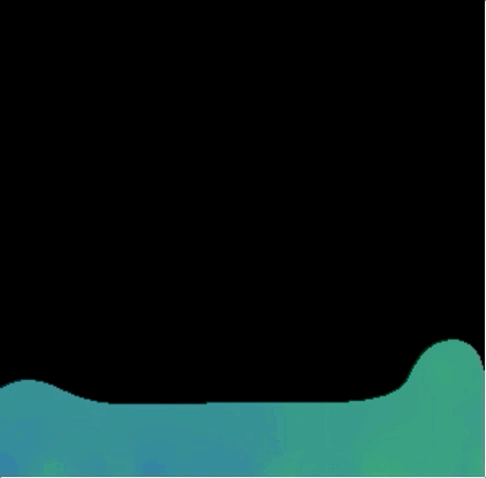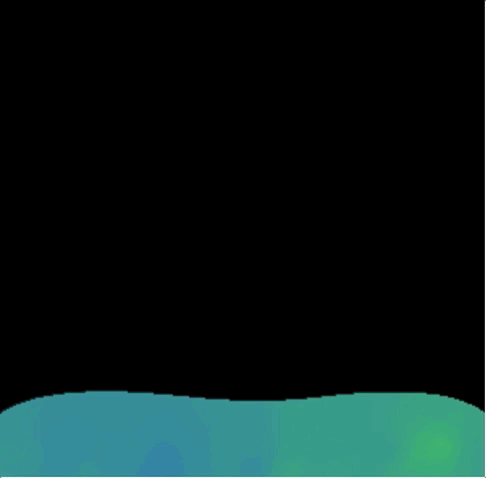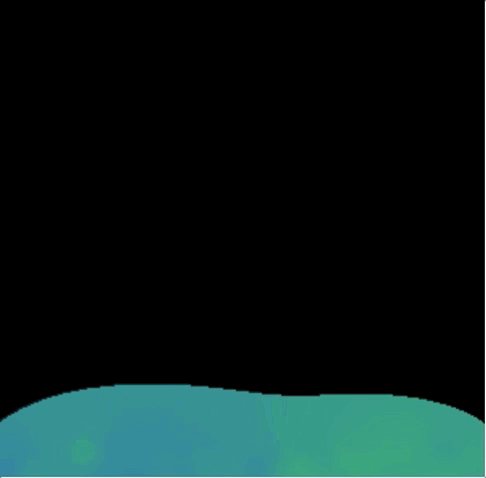
simulation with viscosity applied

User Interaction Forces

Applying user interaction forces consisted of two steps: the first was identifying the location, movement, and clicking of a mouse on the canvas. The second was creating a force around the cursor that would propel the water particles outwards when the mouse was clicked.

By tracking the movement and click of the mouse on our web window, we were able to note the relative coordinates of the mouse. These were then passed into a function that was called throughout the duration of the user clicking on the screen. Then, iterating through all of the particles on the screen, we applied an outward force on each particle with magnitude relative to the distance from the coordinates of the mouse to that particle. Thus each particle was propelled outwards restricted by a defined constraint parameter (to make the simulation more realistic and to potentially prevent the particles from being pushed out too far).

simulation with user interactions

Real-Time Simulation and Rendering

To make the simulation run in real-time in the browser, we implemented the algorithm in Rust and compiled it to WebAssembly. Some problems we ran into were Rust’s variable borrowing/mutability issues. Since most of the group was still new to the language, we ran into lots of bugs caused by Rust-specific issues. We learned how to work around these bugs and language specific limitations (such as double borrowing a variable, figuring out how to copy a variable’s contents to avoid such issues, etc). We also used WebGL2, which allowed us to implement the metaball rendering algorithm completely in the browser by passing floating point positions of each particle as a uniform texture parameter to the fragment shader. Then, when rendering each point we simply looped over all the particles in the simulation to calculate the color at that point.

Lessons Learned

We learned a lot about both simulation and rendering through this project. One of the biggest takeaways was how challenging it is to maintain accuracy while trying to get real-time simulation results. In order to achieve high performance, we decided to implement double density relaxation and viscosity with a particle-based system, but this introduced many parameters that are difficult to tune. In addition, we had to balance performance versus instability since we used a forward Euler integration technique. We also learned about how to effectively use GPUs to optimize rendering by using WebGL to render particles to the screen. Even with our GPU acceleration, a very large number of particles (~5000) causes the application to become sluggish which demonstrates how much effort must be put into production applications to render high quality results while maintaining performance. Finally, we learned about the challenges and benefits of using system programming languages like Rust, which enforce restrictions on code architecture but produce efficient code that allowed our simulation to run in real-time.

Results

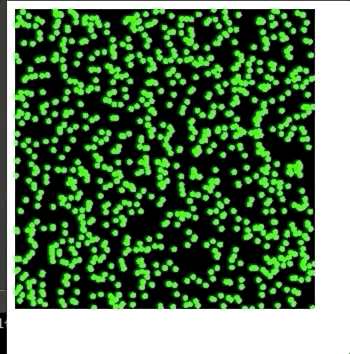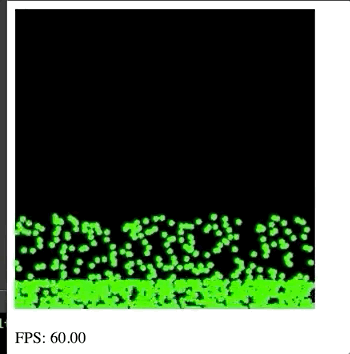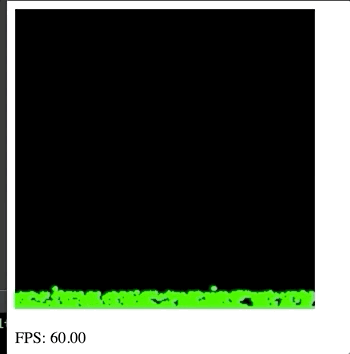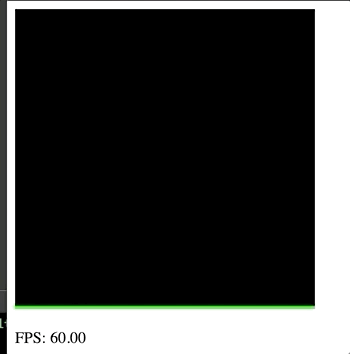
Since the goal of the project is to run in the browser, we've embedded the final application below as an interactive frame!

In case you can't run the simulation, here's a GIF of what it looks like in action!

final simulation with user interactions

References

Contributions